
With the Bayes filter code from lab 7, it is time to actually run it and find the bugs.
Since the code I wrote for lab 7 was basically functional, I simply had to fix a few typos (when I used loc instead of mapper or Mapper instead of mapper), and I was able to start debugging. One of the most crucial bugs I found was that I was not using world coordinates in places where I should have been. Therefore, the entire prediction is problematic. It is interesting, however, that I did not discover this problem until much later on. The updating step has much more of an impact on the final position and my beliefs were actually pretty close to the ground truth. Here is the plot after fixing that error.
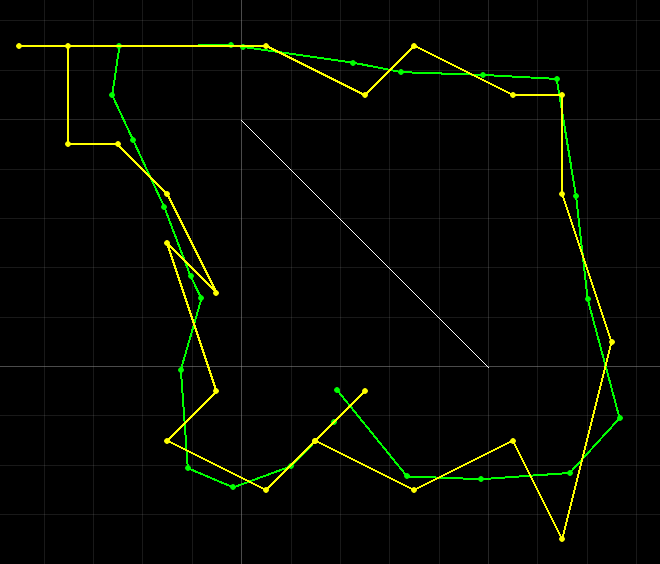
As we can see, the localization results are actually pretty good. An important distinction between Bayes and simply odometry is that the error does not accumulate since we only really use the difference between odometries. Comparing the scans with the ground truth afterwards makes the localization much more accurate. At the end, after all the steps, the indices are only slightly off with GT index = (11, 8, 10) and Bel index = (12, 9, 10). However, I believe that there is still something slightly off with my algorithm and the results can be improved. Below is the modified Bayes filter code.
# In the docstring, "Pose" refers to a tuple (x,y,yaw) in (meters, meters, degrees)
# In world coordinates
def compute_control(cur_pose, prev_pose):
""" Given the current and previous odometry poses, this function extracts
the control information based on the odometry motion model.
Args:
cur_pose ([Pose]): Current Pose
prev_pose ([Pose]): Previous Pose
Returns:
[delta_rot_1]: Rotation 1 (degrees)
[delta_trans]: Translation (meters)
[delta_rot_2]: Rotation 2 (degrees)
"""
cur_x, cur_y, cur_a = cur_pose
prev_x, prev_y, prev_a = prev_pose
delta_trans = ( (cur_y-prev_y)**2 + (cur_x-prev_x)**2 )**0.5
deg = math.atan2(cur_y-prev_y, cur_x-prev_x)
delta_rot_1 = deg - prev_a
delta_rot_2 = cur_a - deg
return delta_rot_1, delta_trans, delta_rot_2
# In world coordinates
def odom_motion_model(cur_pose, prev_pose, u):
""" Odometry Motion Model
Args:
cur_pose ([Pose]): Current Pose
prev_pose ([Pose]): Previous Pose
(rot1, trans, rot2) (float, float, float): A tuple with control data in the format
format (rot1, trans, rot2) with units (degrees, meters, degrees)
Returns:
prob [float]: Probability p(x'|x, u)
"""
d = compute_control(cur_pose,prev_pose)
p1 = max(loc.gaussian(d[0]-u[0],0,loc.odom_rot_sigma),loc.gaussian(d[0]-u[0]-360,0,loc.odom_rot_sigma),loc.gaussian(d[0]-u[0]+360,0,loc.odom_rot_sigma))
p2 = loc.gaussian(d[1]-u[1],0,loc.odom_trans_sigma)
p3 = max(loc.gaussian(d[2]-u[2],0,loc.odom_rot_sigma),loc.gaussian(d[2]-u[2]-360,0,loc.odom_rot_sigma),loc.gaussian(d[2]-u[2]+360,0,loc.odom_rot_sigma))
prob = p1 * p2 * p3
return prob
def prediction_step(cur_odom, prev_odom):
""" Prediction step of the Bayes Filter.
Update the probabilities in loc.bel_bar based on loc.bel from the previous time step and the odometry motion model.
Args:
cur_odom ([Pose]): Current Pose
prev_odom ([Pose]): Previous Pose
"""
u = compute_control(cur_odom, prev_odom)
for i in range(mapper.MAX_CELLS_X):
for j in range(mapper.MAX_CELLS_Y):
for k in range(mapper.MAX_CELLS_A):
loc.bel_bar[i,j,k] = 0
for i1 in range(mapper.MAX_CELLS_X):
for j1 in range(mapper.MAX_CELLS_Y):
for k1 in range(mapper.MAX_CELLS_A):
if loc.bel[i1,j1,k1] < 0.0001:
continue
loc.bel_bar[i,j,k] += loc.bel[i1,j1,k1] * odom_motion_model(mapper.from_map(i,j,k),mapper.from_map(i1,j1,k1),u)
def sensor_model(obs, cur_pose):
""" This is the equivalent of p(z|x).
Args:
obs ([ndarray]): A 1D array consisting of the measurements made in rotation loop
Returns:
[ndarray]: Returns a 1D array of size 18 (=loc.OBS_PER_CELL) with the likelihood of each individual measurements
"""
views = mapper.obs_views[cur_pose[0],cur_pose[1],cur_pose[2]]
prob_array = loc.gaussian(views-obs,0,loc.sensor_sigma)
return prob_array
def update_step():
""" Update step of the Bayes Filter.
Update the probabilities in loc.bel based on loc.bel_bar and the sensor model.
"""
loc.get_observation_data()
obs_data = loc.obs_range_data
for i in range(mapper.MAX_CELLS_X):
for j in range(mapper.MAX_CELLS_Y):
for k in range(mapper.MAX_CELLS_A):
acc = 1
prob_array = sensor_model(obs_data, (i,j,k))
if (loc.bel_bar[i,j,k] == 0):
continue
for l in range(mapper.OBS_PER_CELL):
acc *= prob_array[l]
loc.bel[i,j,k] = loc.bel_bar[i,j,k] * acc
loc.bel /= np.sum(loc.bel)